Momen Gaya
Pada gerak lurus atau gerak translasi, faktor yang menyebabkan adanya gerak adalah gaya (F). Sedangkan pada gerak rotasi atau gerak melingkar, selain gaya (F), ada faktor lain yang menyebabkan benda itu bergerak rotasi yaitu lengan gaya (l) yang tegak lurus dengan gaya.
Secara matematis, momen gaya dirumuskan
τ = F x l
τ = F . l
Jika antara lengan gaya l dan gaya F tidak tegak lurus maka
τ = F . l sin θ
dimana θ adalah sudut antara lengan gaya l dengan gaya F.
Lengan gaya merupakan jarak antara titik tumpuan atau poros ke titik dimana gaya itu bekerja. Jika gaya dikenakan berada di ujung lengan maka bisa kita katakan lengan gaya ( l ) sama dengan jari-jari lingkaran (r).
Sehingga momen gaya dapat juga kita tulis
τ = F . r
Pada penjelasan di atas, arah gaya F1 dan F2 tegak lurus pintu. Kali ini kita mencoba melihat beberapa kondisi yang berbeda. Perhatikan gambar di bawah.
Gambar pintu (dilihat dari atas). Pada gambar a, garis kerja gaya tegak lurus terhadap r (garis kerja gaya membentuk sudut 90o). Pada gambar b, garis kerja gaya membentuk sudut teta terhadap r. Pada Gambar c, garis kerja gaya berhimpit dengan r (garis kerja gaya menembus sumbu rotasi). Walaupun besar gaya sama, tapi karena arah gaya berbeda, maka besar lengan gaya juga berbeda. Lengan gaya l1 lebih besar dari lengan gaya l2. Sedangkan lengan gaya l3 = 0 karena garis kerja gaya F3 berhimpit dengan sumbu rotasi.
Untuk menentukan lengan gaya, kita bisa menggambarkan garis dari sumbu rotasi menuju garis kerja gaya, di mana garis dari sumbu rotasi harus tegak lurus alias membentuk sudut siku-siku dengan garis kerja gaya.
Persamaan Lengan Gaya
Untuk membantu menurunkan persamaan lengan gaya, gurumuda menggunakan bantuan gambar
Amati gambar di atas. Garis kerja gaya membentuk sudut teta terhadap r.
Apabila garis kerja gaya tegak lurus r (gambar a), maka besar lengan gaya adalah :
Apabila garis kerja gaya berhimpit dengan r (gambar c), maka besar lengan gaya adalah :
BESAR TORSI
Torsi adalah hasil kali antara gaya dan lengan gaya. Secara matematis, torsi dirumuskan sebagai berikut :
Jika arah gaya tegak lurus r, maka sudut yang dibentuk adalah 90o. Dengan demikian, besar Torsi untuk kasus ini adalah :
Jika arah gaya berhimpit dengan r, maka sudut yang dibentuk adalah 0o. Dengan demikian, besar Torsi untuk kasus ini adalah :
Para fisikawan sering menggunakan istilah torsi sedangkan para insnyur sering menggunakan istilah Momen Gaya.
Satuan Sistem Internasional untuk Torsi adalah Newton meter. Satuan Torsi tetap Newton meter, bukan joule, karena torsi bukan energi.
ARAH TORSI
Torsi merupakan besaran vector, sehingga selain mempunyai besar, torsi juga mempunyai arah. Apabila arah rotasi berlawanan dengan putaran jarum jam, maka Torsi bernilai positif. Sebaliknya, apabila arah rotasi searah dengan putaran jarum jam, maka arah torsi bernilai negative. Untuk menentukan arah torsi, kita menggunakan kaidah alias aturan tangan kanan. Untuk mempermudah pemahamanmu, perhatikan gambar di bawah.
Pintu didorong ke depan
Catatan :
Arah gaya F pada gambar di bawah tidak tegak lurus ke atas alias tidak menuju ke langit. Arah gaya menembus pintu. Jadi pintunya dilihat dari atas. Bayangkanlah dirimu mendorong pintu ke depan, di mana arah doronganmu tegak lurus pintu itu.
Gambar pintu (dilihat dari atas). Misalnya kita mendorong pintu dengan gaya F, di mana arah gaya tegak lurus r. Bagaimana-kah arah Torsi untuk kasus ini ? gampang… Gunakan aturan tangan kanan. Rentangkan jari tangan kanan dan usahakan supaya posisi keempat jari tangan kanan sejajar dengan arah gaya F. setelah itu, putar keempat jari tangan kanan menuju sumbu rotasi (ke kiri). Arah yang ditunjukkan oleh Ibu Jari adalah arah Torsi. Untuk contoh di atas, putaran keempat jari tangan kanan berlawanan dengan putaran jarum jam. Arah torsi tegak lurus ke atas (menuju langit)
Pintu didorong ke belakang
Catatan :
Arah gaya F pada gambar di bawah tidak tegak lurus ke bawah alias tidak menuju ke tanah. Arah gaya menembus pintu. Bayangkanlah dirimu mendorong pintu dari depan, di mana arah doronganmu tegak lurus pintu itu.
Gunakan aturan tangan kanan lagi untuk menentukan arah torsi. Rentangkan jari tangan kanan dan usahakan supaya posisi keempat jari tangan kanan sejajar dengan arah gaya F. setelah itu, putar keempat jari tangan kanan menuju sumbu rotasi. Arah yang ditunjukkan oleh Ibu Jari adalah arah Torsi. Untuk kasus ini, putaran keempat jari tangan kanan searah dengan putaran jarum jam. Arah torsi tegak lurus ke bawah (menuju ke dalam tanah). Arah Torsi bernilai negative karena putaran searah dengan arah putaran jarum jam.
|
|
| Momen Inersia Rotasi Benda Tegar Momen Inersia Misalnya sebuah partikel bermassa m diberikan gaya F sehingga ia melakukan gerak rotasi terhadap sumbu O. Partikel itu berjarak r dari sumbu rotasi. mula-mula partikel itu diam (kecepatan = 0). Setelah diberikan gaya F, partikel itu bergerak dengan kecepatan linear tertentu. Mula-mula partikel diam, lalu bergerak (mengalami perubahan kecepatan linear) setelah diberikan gaya. Dalam hal ini benda mengalami percepatan tangensial. Percepatan tagensial = percepatan linear partikel ketika berotasi. Kita bisa menyatakan hubungan antara gaya (F), massa (m) dan percepatan tangensial (at), dengan persamaan Hukum II Newton : Karena partikel itu melakukan gerak rotasi, maka ia pasti mempunyai percepatan sudut. Hubungan antara percepatan tangensial dengan percepatan sudut dinyatakan dengan persamaan : Sekarang kita masukan a tangensial ke dalam persamaan di atas : Kita kalikan ruas kiri dan ruas kanan dengan r : Perhatikan ruas kiri. rF = Torsi, untuk gaya yang arahnya tegak lurus sumbu (bandingan dengan gambar di atas). Persamaan ini bisa ditulis menjadi : mr2 adalah momen inersia partikel bermassa m, yang berotasi sejauh r dari sumbu rotasi. persamaan ini juga menyatakan hubungan antara torsi, momen inersia dan percepatan sudut partikel yang melakukan gerak rotasi. Istilah kerennya, ini adalah persamaan Hukum II Newton untuk partikel yang berotasi.
Jadi Momen Inersia partikel merupakan hasil kali antara massa partikel itu (m) dengan kuadrat jarak tegak lurus dari sumbu rotasi ke partikel (r2). Untuk mudahnya, bandingkan dengan gambar di atas. Secara matematis, momen inersia partikel dirumuskan sebagai berikut : Momen Inersia Benda Tegar Secara umum, Momen Inersia setiap benda tegar bisa dinyatakan sebagai berikut : Benda tegar bisa kita anggap tersusun dari banyak partikel yang tersebar di seluruh bagian benda itu. Setiap partikel-partikel itu punya massa dan tentu saja memiliki jarak r dari sumbu rotasi. jadi momen inersia dari setiap benda merupakan jumlah total momen inersia setiap partikel yang menyusun benda itu. Ini cuma persamaan umum saja. Bagaimanapun untuk menentukan Momen Inersia suatu benda tegar, kita perlu meninjau benda tegar itu ketika ia berotasi. Walaupun bentuk dan ukuran dua benda sama, tetapi jika kedua benda itu berotasi pada sumbu alias poros yang berbeda, maka Momen Inersia-nya juga berbeda. Sekarang coba kita lihat Momen Inersia beberapa benda tegar. Momen Inersia Benda-Benda yang Bentuknya Beraturan Selain bergantung pada sumbu rotasi, Momen Inersia (I) setiap partikel juga bergantung pada massa (m) partikel itu dan kuadrat jarak (r2) partikel dari sumbu rotasi. Total massa semua partikel yang menyusun benda = massa benda itu. Persoalannya, jarak setiap partikel yang menyusun benda tegar berbeda-beda jika diukur dari sumbu rotasi. Ada partikel yang berada di bagian tepi benda, ada partikel yang berada dekat sumbu rotasi, ada partikel yang sembunyi di pojok bawah, ada yang terjepit di tengah . amati gambar di bawah Ini contoh sebuah benda tegar. Benda-benda tegar bisa dianggap tersusun dari partikel-partikel. Pada gambar, partikel diwakili oleh titik berwarna hitam. Jarak setiap partikel ke sumbu rotasi berbeda-beda. Ini cuma ilustrasi saja.
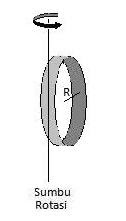
Lingkaran tipis dengan jari-jari R dan bermassa M (sumbu rotasi terletak pada pusat) Lingkaran tipis ini mirip seperti cincin tapi cincin lebih tebal. Jadi semua partikel yang menyusun lingkaran tipis berada pada jarak r dari sumbu rotasi. Momen inersia lingkaran tipis ini sama dengan jumlah total momen inersia semua partikel yang tersebar di seluruh bagian lingkaran tipis. Momen Inersia lingkaran tipis yang berotasi seperti tampak pada gambar di atas, bisa diturunkan sebagai berikut : Perhatikan gambar di atas. Setiap partikel pada lingkaran tipis berada pada jarak r dari sumbu rotasi. dengan demikian : r1 = r2 = r3 = r4 = r5 = r6 = R I = MR2 Cincin tipis berjari-jari R, bermassa M dan lebar L (sumbu rotasi terletak di tengah-tengah salah satu diameter) Cincin tipis berjari-jari R, bermassa M dan lebar L (sumbu rotasi terletak pada salah satu garis singgung) Silinder berongga, dengan jari-jari dalam R2 dan jari-jari luar R1 Silinder padat dengan jari-jari R (sumbu rotasi terletak pada sumbu silinder) Silinder padat dengan jari-jari R (sumbu rotasi terletak pada diameter pusat) Bola pejal dengan jari-jari R (sumbu rotasi terletak pada salah satu diameter) Kulit Bola dengan jari-jari R (sumbu rotasi terletak pada salah satu diameter) Batang pejal yang panjangnya L (sumbu rotasi terletak pada pusat ) Batang pejal yang panjangnya L (sumbu rotasi terletak pada salah satu ujung) Balok pejal yang panjangnya P dan lebarnya L (sumbu rotasi terletak pada pusat; tegak lurus permukaan) |
| Energi Kinetik Rotasi Jika energi kinetik translasi merupakan energi yang dimiliki oleh benda-benda yang bergerak pada lintasan lurus, maka energi kinetik rotasi merupakan energi yang dimiliki oleh benda yang melakukan gerak rotasi. Bedanya, dalam gerak lurus kita menganggap setiap benda sebagai partikel tunggal, sedangkan dalam gerak rotasi, setiap benda dianggap sebagai benda tegar (Benda dianggap terdiri dari banyak partikel. Ketika benda tegar berotasi, semua partikel yang tersebar di seluruh bagian benda itu juga berotasi. Ingat bahwa setiap partikel mempunyai massa (m). Ketika benda tegar berotasi, setiap partikel itu juga bergerak dengan kecepatan (v) tertentu. Kecepatan setiap partikel bergantung pada jaraknya dari sumbu rotasi. Semakin jauh sebuah partikel dari sumbu rotasi, semakin cepat partikel itu bergerak (kecepatannya besar). Sebaliknya, semakin dekat partikel dari sumbu rotasi, semakin lambat partikel itu bergerak (kecepatannya kecil). Ketika kita mendorong pintu, pintu juga berotasi alias berputar pada sumbu. Engsel yang menghubungkan pintu dengan tembok berfungsi sebagai sumbu rotasi. (kecepatannya lebih besar). Sebaliknya, bagian pintu yang berada di dekat engsel bergerak lebih pelan (kecepatannya lebih kecil). Jadi ketika sebuah benda berotasi, kecepatan (v) setiap partikel berbeda-beda, tergantung jaraknya dari sumbu rotasi. Karena setiap partikel mempunyai massa (m) dan kecepatan (v), maka kita bisa mengatakan bahwa ketika sebuah benda tegar berotasi, semua partikel yang menyusun benda itu memiliki energi kinetik (energi kinetik = energi kinetik translasi… jangan lupa ya). Nah, total energi kinetik semua partikel yang menyusun benda tegar = energi kinetik benda tegar. Secara matematis, bisa ditulis sebagai berikut : EK benda tegar = Total semua Energi Kinetik partikel EK benda tegar = EK1 + EK2 + EK3 + …. + EKn EK benda tegar = ½ m1v12 + ½ m2v22 + ½ m3v32 + …. + ½ mnvn2 Keterangan : EK1 = ½ m1v12 = Energi Kinetik Partikel 1 EK2 = ½ m2v22 = Energi Kinetik Partikel 2 EK3 = ½ m3v32 = Energi Kinetik Partikel 3 Karena partikel yang menyusun benda tegar sangat banyak, maka kita cukup menulis titik-titik (…..) EKn = ½ mnvn2 = Energi Kinetik partikel yang terakhir Persamaan di atas bisa kita tulis lagi seperti ini : Walaupun kecepatan linear setiap partikel berbeda-beda, kecepatan sudut semua partikel itu selalu sama. Dengan kata lain, ketika sebuah benda tegar berotasi, kecepatan sudut semua bagian benda itu selalu sama. Hubungan antara kecepatan linear dan kecepatan sudut, dinyatakan dengan persamaan : Karena kecepatan sudut semua partikel sama, maka persamaan ini bisa ditulis menjadi : Ini adalah persamaan energi kinetik rotasi benda tegar… Satuan energi kinetik rotasi = joule, seperti bentuk energi lainnya… |
Katrol Tetap
Pada Katrol Tetap Titik Tumpu terletak pada sumbu katrol artinya Jarak antara Titik Beban ke Titik Tumpu sama dengan jarak antara kuasa ke titik tumpu dengan demikian maka panjang lengan beban sama dengan panjang lengan kuasa
Karena Lengan beban sama dengan Lengan Kuasa
Maka keuntungan mekanik pada katrol tetap adalah :
Jadi keuntungan mekanik katrol tetap adalah 1
Keuntungan lain dari katrol tetap adalah mengubah arah gaya dari gaya angkat menjadi gaya tarik ke bawah
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|